![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
太田研 公開用Wiki
現在,編集途中です・・・ 鋭意製作中ですっ!!
貴方はこのページの5384人目の目撃者です.
このページでは, 私が学部4年で行った卒業研究の概略を紹介してゆきます. 分野はコンピュータグラフィックスで, 内容は簡単に説明すると, 人間が見た時に対象とする物体の特徴が一番わかりやすい陰影がつくような光の当て方の自動計算を行うための方法についてです.
コンピュータグラフィックスでは, 画像を生成するにあたり視点, 光源位置, 物体位置等を 設定する必要がある. これらのパラメータは生成される画像の出来栄えに大きな影響を及ぼ す. しかし, 生成された画像に対する出来栄えの評価は個々人の目的によって変わる. 映画や ゲーム, 芸術といった目的ではどのような視点, 光源位置が良いかは, 制作者の意図によって 大きく変わるが, 設計や製品デザインなど物体の形状情報を詳細に伝えたいという目的があ る分野では, 物体の形状特徴を良く表現できる視点位置, 光源位置を選択する必要がある. 一般的に, コンピュータグラフィックスによる三次元の情報は紙面, ディスプレイといった 二次元の媒体を通して人間に伝達される. その際, 視点や照明条件は伝達できる描画対象の 物体の持つ三次元的情報の量を大きく左右することになる. よって, 物体の持つ三次元的な 情報をより多く詳細に伝達したい場合, 視点位置, 光源位置の選択は重要な問題となる.
科学的可視化の分野では, 科学的可視化の基本概念である情報量の最大化の考えに基づき, 物体の形状特徴を良く伝達できる視点の自動計算の研究がされている. また, この考えを応 用し, 次のような最適なライティングパラメータを自動計算する研究も存在する. 照明デザイン(Lighting Design) の分野では, シーンに対して最も良い照明パラメータ(色, 方 向, 明るさ) を設定することが求められる, しかし, それらのパラメータを決定することは非 常に難しく, 多大な労力と時間を要する. このことに対する部分的な解決案として, 照明から の情報量を最大化するという考えに基づいた最適な光源位置の選択法が研究がされている. 本研究では, 最適な光源位置の選択法について, 既存の方法に, 対象物の持つ凹凸や奥行き の情報が, 画像の輝度の変化として表現されているかという視点からの評価を加えることに より, 対象物の詳細な形状情報を伝達することが重要であるような, 製品広告の分野やCAD の完成図などのへの応用を目指した最適な光源配置を行うための, より良い照明条件の評価 法を提案する.
 |  |
| 図1.2.1 良い光源位置による画像 | 図1.2.2 悪い光源位置による画像 |
物体に最適な陰影表現を施すような光源位置を探索するためには,照明条件の評価が必要である.
照明条件を評価するために既存の手法では,描画された画像の輝度*1の分布の情報エントロピー*2を用いた.すなわち,画像に暗い色から明るい色まで満遍なく現れているかという指標である.
既存手法の評価値は,大まかには以下の手順で計算される.





 |  |
| 図2.1.1 | 図2.1.2 |
物体が光に照らされたとき,物体表面のカーブしている部分は明るい色から暗い色へ連続的に変化するような陰影が生じる.その色の明るさの変化によって人間はその部分に奥行きを感じ,その部分がカーブしていると認識する*4.
 |
| 図3.1 色の明るさの変化による奥行きの知覚 |
既存手法で問題となったのは,物体表面に真っ黒い影ができてその部分の凹凸情報などが判らなくなってしまったことである.すなわち,曲面になっている部分でも黒く塗りつぶされていて色の明るさの変化が無いため,その部分の形状の認識を阻害してしまうことになる.
よって,物体を描画した際に,物体の曲面部分にちゃんと輝度の変化(色の明るさの変化)が現れているかという指標を考える.
さらに,これに描画された画像のコントラストに対する指標を用いる。コントラストは,色の違いが分かりやすくなり,人間が見た時,より立体感を感じやすくなる.
よって,
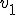 を輝度の変化の仕方に対する評価値とし,
を輝度の変化の仕方に対する評価値とし,
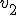 を画像のコントラストに対する評価値とし,
を画像のコントラストに対する評価値とし,
新たな照明条件の評価値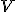 を以下の式で計算する.
を以下の式で計算する.
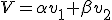
この指標は,物体の詳細な部分が輝度の連続的な変化として現れているかという指標と
物体に奥行きを与えるようなコントラストが得られるかという指標の重み付きの和となっている.
コントラストに対する指標である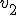 は,既存手法のエントロピーを計算することにより評価が可能である.
は,既存手法のエントロピーを計算することにより評価が可能である.
よって,今回は物体の詳細な部分が輝度の連続的な変化として現れているかという指標である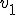 の計算法を2種類提案する.
の計算法を2種類提案する.
編集中...
 |  |
| 図3.1.1 画像a | 図3.1.2 エントロピーの変化のグラフ |
 |  |  |
| 図3.1.3 ヒストグラム(32階調) | 図3.1.4 ヒストグラム(16階調) | 図3.1.5 ヒストグラム(8階調) |
 |  |
| 図3.1.6 画像b | 図3.1.7 エントロピーの変化のグラフ |
 |  |  |
| 図3.1.8 ヒストグラム(32階調) | 図3.1.9 ヒストグラム(16階調) | 図3.1.10 ヒストグラム(8階調) |
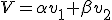
編集中...
 |  |
| 図3.2.1 画像a | 図3.2.2 エントロピーの変化のグラフ |
 |  |  |
| 図3.2.3 ヒストグラム | 図3.2.4 ヒストグラム(平滑化後①) | 図3.2.5 ヒストグラム(平滑化後②) |
 |  |
| 図3.2.6 画像b | 図3.2.7 エントロピーの変化のグラフ |
 |  |  |
| 図3.2.8 ヒストグラム | 図3.2.9 ヒストグラム(平滑化後①) | 図3.2.10 ヒストグラム(平滑化後②) |
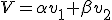
編集中...
それぞれの評価値を用いて実験を行なった結果を以下に示す.
| モデルネーム | 既存手法 | 提案手法(1) | 提案手法(2) |
| stanford bunny |  |  |  |
| stanford dragon |  |  |  |
| happy buddha |  |  |  |
編集中...
| 全体的な奥行き | 表面の凹凸 | |
| 既存手法 | ◎ | △ |
| 提案手法(1) | △ | 〇 |
| 提案手法(2) | 〇 | 〇 |